Can you find the next number in this sequence?
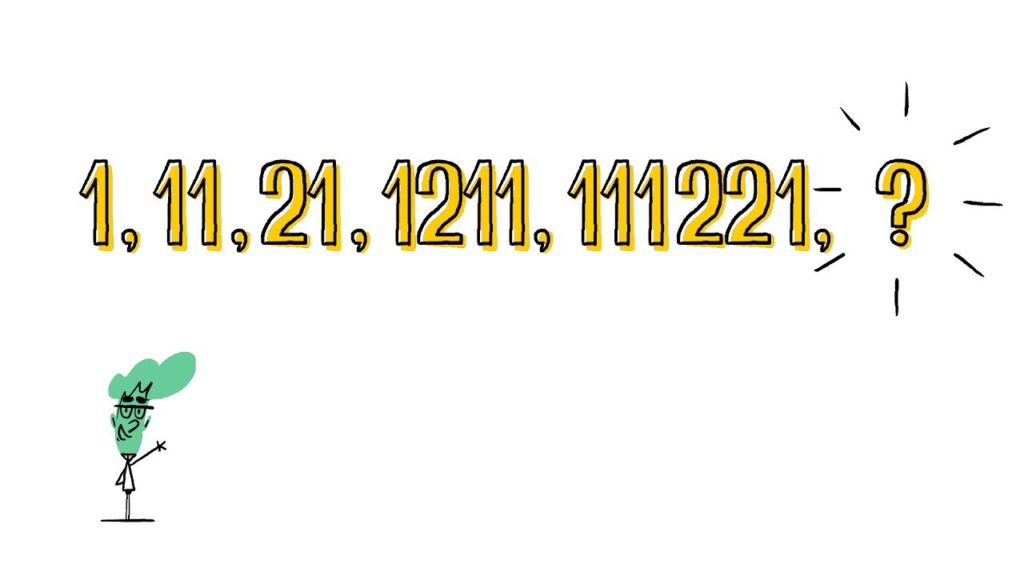
These are the first five elements of a number sequence. Can you figure out what comes next? Pause here if you want to figure it out for yourself. Answer in: 3 Answer in: 2 Answer in: 1 There is a pattern here, but it may not be the kind of pattern you think it is. Look at the sequence again and try reading it aloud. Now, look at the next number in the sequence. 3, 1, 2, 2, 1, 1. Pause again if you’d like to think about it some more. Answer in: 3 Answer in: 2 Answer in: 1 This is what’s known as a look and say sequence.
Unlike many number sequences, this relies not on some mathematical property of the numbers themselves, but on their notation. Start with the left-most digit of the initial number. Now, read out how many times it repeats in succession followed by the name of the digit itself. Then move on to the next distinct digit and repeat until you reach the end. So the number 1 is read as “one one” written down the same way we write eleven.
Of course, as part of this sequence, it’s not actually the number eleven, but 2 ones, which we then write as 2 1. That number is then read out as 1 2 1 1, which written out we’d read as one one, one two, two ones, and so on. These kinds of sequences were first analyzed by mathematician John Conway, who noted they have some interesting properties. For instance, starting with the number 22, yields an infinite loop of two twos.
But when seeded with any other number, the sequence grows in some very specific ways. Notice that although the number of digits keeps increasing, the increase doesn’t seem to be either linear or random. In fact, if you extend the sequence infinitely, a pattern emerges. The ratio between the amount of digits in two consecutive terms gradually converges to a single number known as Conway’s Constant. This is equal to a little over 1.3, meaning that the amount of digits increases by about 30% with every step in the sequence.
What about the numbers themselves? That gets even more interesting. Except for the repeating sequence of 22, every possible sequence eventually breaks down into distinct strings of digits. No matter what order these strings show up in, each appears unbroken in its entirety every time it occurs.
Conway identified 92 of these elements, all composed only of digits 1, 2, and 3, as well as two additional elements whose variations can end with any digit of 4 or greater. No matter what number the sequence is seeded with, eventually, it’ll just consist of these combinations, with digits 4 or higher only appearing at the end of the two extra elements, if at all.
Beyond being a neat puzzle, the look and say sequence has some practical applications. For example, run-length encoding, a data compression that was once used for television signals and digital graphics, is based on a similar concept. The amount of times a data value repeats within the code is recorded as a data value itself. Sequences like this are a good example of how numbers and other symbols can convey meaning on multiple levels.






Responses